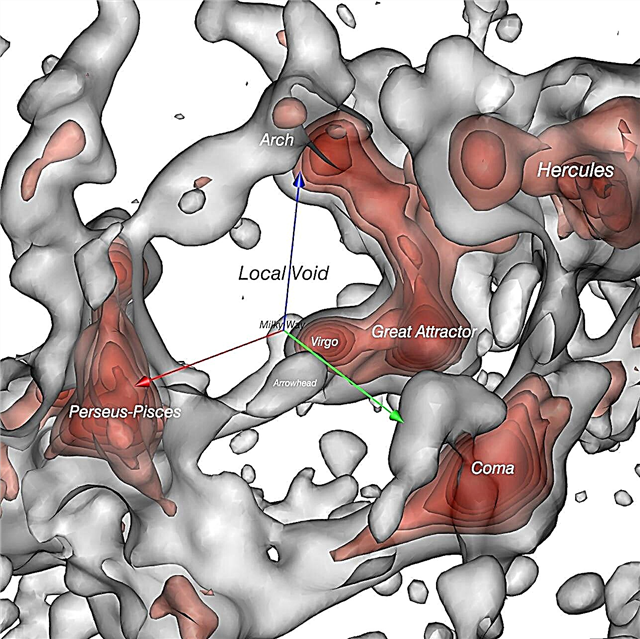
Podpis: Widok księżyca na perygeum i apogeum
Jako nauczyciel zawsze szukam laboratoriów z prostymi ustawieniami odpowiednimi dla studentów. Moim ulubionym jest znalezienie prędkości światła z czekoladą.
W nowym artykule przesłanym niedawno do arXiv Kevin Krisciunas z Teksasu A&M opisuje metodę określania mimośrodowości orbity Księżyca z zaskakująco niskim błędem przy użyciu niczego poza miernikiem, kawałkiem kartonu i programem przeznaczonym do dopasowania krzywych do gwiazdy zmienne.
W tej metodzie wykorzystuje się fakt, że mimośrodowość można określić na podstawie stosunku średniego rozmiaru kątowego obiektu do połowy jego amplitudy. Zatem głównym celem jest zmierzenie tych dwóch wielkości.
Strategia Kevina polega na tym, aby skorzystać z tekturowej dziury celowniczej, która może przesuwać się po drążku metrowym. Patrząc przez dziurę w księżycu i przesuwając kartę tam iz powrotem, aż kątowy rozmiar dziury po prostu zachodzi na księżyc. Stamtąd średnica otworu podzielona przez odległość w dół miernika daje rozmiar kątowy dzięki formule małego kąta (? = D / D w radianach, jeśli D >> d).
Aby uniknąć systematycznych błędów w błędnym osądzaniu, gdy karta jest przesuwana do przodu, aż rozmiar dziury pasuje do księżyca, najlepiej jest podejść do niej również z drugiej strony; Wchodzi z drugiego końca miernika. Powinno to pomóc zmniejszyć liczbę błędów, a Kevin stwierdził, że ma przy tym typowy rozrzut ± 4 mm.
W tym momencie należy wziąć pod uwagę jeszcze jeden błąd systematyczny: źrenica ma skończony rozmiar porównywalny z dziurą obserwacyjną. Spowoduje to, że rzeczywisty rozmiar kątowy będzie niedoszacowany. Jako taki konieczny jest współczynnik korygujący.
Aby wyliczyć ten współczynnik korekcji, Kevin umieścił dysk 91 mm w odległości 10 metrów (powinno to dać dysk o takim samym rozmiarze kątowym jak księżyc patrząc z tej odległości). Aby uzyskać najlepsze dopasowanie, poślizg kartonu z otworem celowniczym powinien należy umieścić na mierniku 681,3 mm, ale z powodu systematycznego błędu źrenicy Kevin uznał, że konieczne jest ustawienie go na 821 mm. Stosunek zaobserwowanego umiejscowienia do właściwego umiejscowienia podał współczynnik korygujący zastosowany przez Kevina (1,205). Musi to zostać skalibrowane dla każdej osoby i będzie również zależeć od ilości światła w czasie obserwacji, ponieważ wpływa to również na średnicę źrenicy. Jednak przyjęcie jednego współczynnika korygującego daje zadowalające wyniki.
Pozwala to na właściwie pobrane dane, które można następnie wykorzystać do ustalenia niezbędnych wielkości (średni rozmiar kątowy i 1/2 amplitudy). Aby je ustalić, Kevin wykorzystał program znany jako PERDET, który jest przeznaczony do dopasowania krzywych sinusoidalnych do oscylacji w gwiazdach zmiennych. Każdy program, który mógłby dopasować takie krzywe do punktów danych za pomocą?2 dopasowanie lub analiza Fouriera byłaby odpowiednia do tego celu.
Z takich programów po określeniu średniej wielkości kąta i połowy amplitudy ich stosunek zapewnia ekscentryczność. W eksperymencie Kevina znalazł wartość 0,039 ± 0,006. Ponadto okres, który określił od perygeum do perygeum, wynosił 27,24 ± 0,29 dnia, co jest doskonale zgodne z przyjętą wartością 27,55 dnia.